2020年9月12日、訂正 SnakeCubeの周波数は3倍になるという予測を2倍に。
またUiからT0iの区間を1サイクルと書いていましたが2サイクルに。
はじめに
2020年3月30日、コンピュータサイエンスに関する米国の学会ACM(Association for Computing Machinery)が、
コロナ感染拡大を受けて同学会の論文が6月30日までオープンアクセスになったようです。
早速、僕が発明したSnakeCubeより優れたものがあるのか調べたところ、
電通大の崎山先生の論文(2007年)が検索でヒットしたのでSnakeCubeと比較をしてSnakeCubeが高速であることを説明します。
崎山先生の論文は、ベルギーのルーヴェン・カトリック大学との共同研究のように見えています。
崎山先生は僕と同時期に日立製作所に勤務されていましたが事業部が違ったので、一度も連絡が取れたことはありません。
以後、「電通大演算器」と呼ばせていただきます。
注意! SnakeCubeはオープンソースではなく商用開発しているものです。
SnakeCubeとは
ICF3-Fと呼んでいたことがありましたがオープンソースと間違われそうなのでSnakeCubeに改名しました。
1999年 RSA暗号の性能で世界一だった暗号LSI ICF3をベースに高速化した巨大整数用四則演算プロセッサです。
汎用演算プロセッサと暗号専用演算器のセットです。僕はICF3の汎用演算プロセッサの唯一の設計、開発者です。
この汎用演算プロセッサに2018年に僕が発明した暗号専用演算器(モンゴメリ乗算器)を追加したもの。
icf.hatenablog.com
米国の学会ACMの次の論文にある演算器のこと。SnakeCubeの演算器に近いところがあります。
「Efficient Pipelining for Modular Multiplication Architectures in Prime Fields」
GLSVLSI’07, March 11-13, 2007, Stresa-Lago Maggiore, Italy.
Copyright 2007 ACM 978-1-59593-605-9/07/0003
演算器の構造について
大雑把な両者の演算器アーキテクチャの話をします。
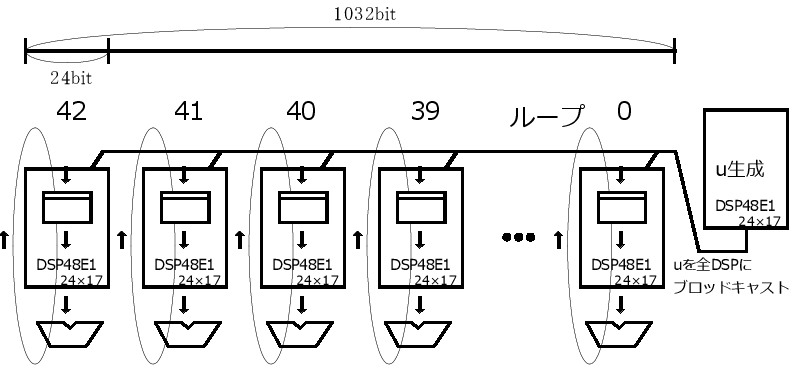
モンゴメリ乗算のループ処理では、巨大整数の乗算を2回するのですが、
SnakeCubeは1個の演算器で直列に2回乗算します。
電通大は1/4個の演算器を2個を使って4回乗算します。
このことから同じ周波数であれば理論的にはSnakeCubeのほうが2倍性能が出ます。
後で説明しますが予想ではSnakeCubeのほうが高い周波数で動作します。
つまり2倍の周波数だとするとSnakeCubeは電通大演算器の4倍高速ということになりますが、
電通大演算器が毎サイクル乗算器を使っているのに対しSnakeCubeでは5サイクルに4回なので、
最終的に3.2倍高速ではないかという予測です。
SnakeCubeの最下位ビットからのブロッドキャストの工夫により、
鍵長が大きくなるにしたがってこの差が、さらに大きくなっていきます。
SnakeCubeが高周波数で動作する秘密
この説明を完全理解するには電通大演算器の論文を読む必要があると思いますが、
このタイプのモンゴメリ乗算器のクリティカルパスは最下位ビットからのブロッドキャストです。
電通大演算器は、このクリティカルパスのために周波数が上がりません。
電通大の論文に書かれている図では、UiからT0iの区間のことで2サイクルになっています。
SnakeCubeでは、このクリティカルパスを3サイクルピッチの4サイクルディレイとなるような工夫をしています。
正しくは3サイクルピッチの4、5・・・nサイクルディレイです。
鍵長が大きくなるにしたがってnが大きくなっていきます。
鍵長が大きくなっても周波数が落ちません。
このため電通大演算器の1.5倍の周波数を見込めるのです。
3サイクルピッチなのですが電通大のUiからT0iに相当するのは4サイクルなので2倍の周波数。
クリティカルパスが3サイクルあるため乗算器は3回に1回しか利用されていないのかというと、
別の演算を1回入れているので、乗算器を3回に2回利用しています。さらに2スレッドにして
クリティカルパスの遅延をオーバーラップさせ5サイクルに4回、乗算器を使うということをします。
まとめ
SnakeCubeは電通大演算器に対して方式性能2倍、周波数2倍。
電通大演算器は乗算器の利用率100%ですがSnakeCubeは80%です。
最終的にSnakeCubeは2×2×0.8 = 3.2倍高速という予想ができました。
また鍵長が大きくなるにしたがってこの差が、さらに大きくなっていきます。