わかりやすいICF3-Fのモンゴメリ乗算器の説明

はじめに

米アマゾンとイーサリアム財団らがFPGAコンテストをするそうです。簡単に言うとA×A mod N (A,N: 1024bit)をできる限り速く演算するというコンテスト。コンテストのサイトで紹介されているサバンチ大学の論文「Low-Latency Modular Multiplication Algorithm - Erdinc Ozturk」にはXilinxのFPGAで剰余乗算器、A×B mod N(A,B,N: 512bit)を実装した結果がある。巨大な剰余乗算器で、ICF3-Fの剰余乗算器(=モンゴメリ乗算器)よりも、かなり高速な演算器です。コンテストで1024bitのものが実装できれば、ですが。コンテストで1024bitの性能の結果が出たようです。詳しくはコンテストのサイトほうへ。

ご注意！　ICF3-Fはオープンソースではありません。

目的

サバンチ大学の論文には128bit、256bit、512bitの結果があるので、そこから1024bitのDSPの数を予想すると4225個。一方、ICF3-Fは44個×2です。 サバンチ大学の論文の方法で1024bitのものが実装されてもICF3-Fは、RSAのSSLアクセラレータの用途など、実際に利用される用途では負けていないということを言いたいのですが、 あまり細かいことを書きたくなかったので、わかりやすいICF3-Fのモンゴメリ乗算器の説明になりました。ICF3-Fとの違いで大きなものはNの入れ替え。 ICF3-Fは演算毎にNを入れ替えられるが、Nの入れ替えに時間がかかると思われます。つまりサバンチ大学の論文では複数のSSL証明書を運用したい場合、運用が難しい。周波数も考慮しないといけないのですがICF3-Fの約100倍のDSPを使うので100倍以上の性能が出ないとコストパフォーマンスが悪い。100倍以上としたのは、ICF3-FはリダクションもDSPで演算していますが、サバンチ大学の論文では巨大なLUTとBRAMを必要としている点があります。サバンチ大学の論文では小型のSSLアクセラレータを作れないであろうとか。

ICF3-Fのモンゴメリ乗算器(1024bit版 DSP 44個)

ICF3-Fのモンゴメリ乗算器

1ループ=3サイクルで17bit分のモンゴメリ乗算。1024×1024bitをするには61ループ(183サイクル)。DSP内のレジスタに入力データを設定、ループ終了後、DSP内のレジスタに答えが格納されている。 uのブロッドキャスト以外は、隣接するDSPしかデータ転送がなくデータのローカリティが高いアーキテクチャ。k番目のDSPは、k-1番目のDSPとk+1番目のDSPと通信するのみで配線実装しやすい。 3サイクル中、乗算は2回行われる。乗算のうち、ひとつはuの値がないと演算できないためDSPが2倍あっても、あまり高速化できない。1つのDSPでuの値が不要な乗算を先に行い、その後、uの値を使う乗算を行う。DSPは乗数を17bitづつシフトする用途にも使われている。サバンチ大学の論文では乗算にRNSを使っているためXilinxのDSPの24×17の乗算器を16×16として使っているがICF3-Fでは乗算にRNSは使っていないので24×17として使えている。つまり(24×17)÷(16×16) = 1.59倍、効率良く乗算器を使っている。

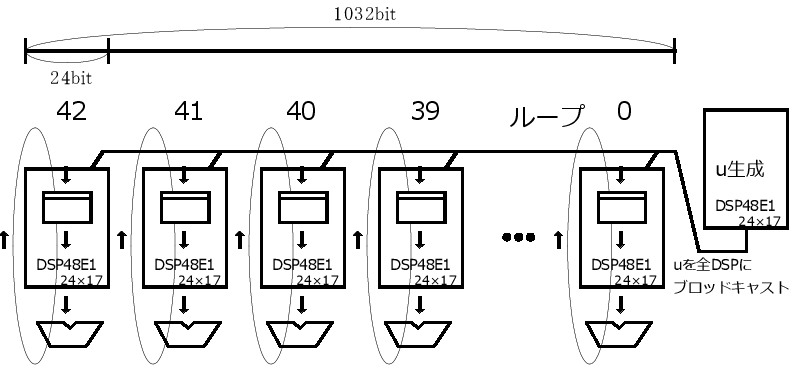
このようにループさせるだけでモンゴメリ乗算が正しく演算できることの証明はモンゴメリ乗算の累積加算における分割加算の証明にあります。

大きなモンゴメリ乗算器が実装できる仕組み

大きなモンゴメリ乗算器が実装できる仕組み

乗算器が大きくなっていくとuのディレイが間に合わなくなってくる。そこでuのブロッドキャストに中継FFを入れる。 kからk+1のデータはFFで中継。k+1からkのデータを1サイクル早く作る。ここがポイント。このときディレイが心配になるが、それでもクリティカルパスはu生成になると思うので、ここはクリティカルパスにならない。このため、途方もなく大きなモンゴメリ乗算器を実装できる。途方もなく大きな乗算器になってもクリティカルパスが、長くなることはない。つまりDSP当たりの演算効率は、ほとんど下がらない。

ICF3-Fの性能を2倍にする

RSA暗号のSSLアクセラレータにおいて、RSA暗号の鍵長が大きくなるとサバンチ大学の論文では実装できなくなるし、ICF3-Fも実装できても性能が遅すぎる問題がでてくる。そこで2個のICF3-Fを連結して中国人剰余定理を使って、性能をほぼ２倍にする方法が、現実可能だということです。